Motion Prediction

Overview
Given agents' tracks for the past 1 second on a corresponding map, predict the positions of up to 8 agents for 8 seconds into the future. To enable the motion prediction challenge, the ground truth future data for the test set is hidden from challenge participants. As such, the test sets contain only 1 second of history data. The validation sets contain the ground truth future data for use in model development. In addition, the test and validation sets provide a list of up to 8 object tracks in the scene to be predicted. These are selected to include interesting behavior and a balance of object types.
Leaderboard
This leaderboard only displays submissions made on or after March 18, 2024, when the 2024 Waymo Open Dataset Challenges start.
With the latest v1.2.1 of the Motion Dataset, Lidar and Camera data is now available for the 1s history data.
[Update March 2024] We have improved the logic behind the behavior bucketing used for mAP. This introduced some marginal changes to the mAP metric which will be reflected in the current leaderboard. Past leaderboards will maintain the scores before this change, and these changes will not impact results of previous challenges. Past leaderboards and challenges are available here.
Note: the rankings displayed on this leaderboard may not accurately reflect the final rankings for this Challenge.
Submit
Submissions are uploaded as serialized MotionChallengeSubmission protos. Each ScenarioPredictions proto within the submission corresponds to a single scenario in the test set and contains up to 8 predictions for the objects listed in the tracks_to_predict field of the scenario. Trajectory predictions must contain exactly 16 position samples each corresponding to the future 8 seconds sampled at 2 Hz. IMPORTANT: note that predictions do not include the current time step so the first prediction sample must correspond to 0.5 seconds into the future (Scenario track step 15), not the current time.
To submit your entry to the leaderboard, upload your file as a serialized MotionChallengeSubmission proto file compressed into a .tar.gz archive file. If the single proto is too large, you can shard them across multiple files where each file contains a subset of the predictions. Then tar and gzip them into a .tar.gz file before uploading.
To be eligible to participate in the Challenge, each individual/all team members must read and agree to be bound by the WOD Challenges Official Rules.
You can only submit against the Test Set 3 times every 30 days. (Submissions that error out do not count against this total.)
Metrics
Leaderboard ranking for this challenge is by the average Soft mAP (see definition below) across evaluation times (3, 5, and 8 seconds) averaged over the individual results for all object types. Miss rate will be used as a secondary metric.
All metrics described below are computed by first bucketing all objects into object type. The metrics are then computed per type. The metrics for each object type (ADE, FDE, Miss Rate, Overlap rate, and mAP) are all computed at 3, 5, and 8 second timestamps.
Definitions
Let G be a set of N agents.
Let K be the number of predicted future trajectories.
Let T be the number of time steps per trajectory.
G is associated with a future trajectory distribution:
\begin{equation}
\big\{(l_{G}^{i} S_{G}^{i})\big\}_{i=1}^{K}
\end{equation}
Where \(l_{G}^{i}\) is an un-normalized likelihood for prediction i.
Where \(S_g^i\) is the predicted trajectory for prediction i.
minADE
Minimum Average Displacement Error
Let \(\hat{s}G^k\) be the ground truth for the agent.
The minADE metric computes the mean of the l2 norm between the ground truth for all agents in G and the closest prediction.
\begin{equation}
\mbox{minADE}(G) = \min_i \frac{1}{T} \sum_{t=1}^{T}||\hat{s}_{G}^{t} - s_{G}^{it}||_2
\end{equation}
Where T is the last prediction time step to include in the metric.
minFDE
Minimum Final Displacement Error
The minFDE metric is equivalent to evaluating the minADE metric at a single time step T:
\begin{equation}
\mbox{minFDE}(G) = \min_i ||\hat{s}_{G}^{T} - s_{G}^{iT}||_2
\end{equation}
Miss Rate
A miss is defined as the state when none of the individual K predictions for an object are within a given lateral and longitudinal threshold of the ground truth trajectory at a given time T.
I.e. For prediction i, the displacement vector at time T is rotated into the ground truth agent coordinate frame.
\begin{equation}
D_j^i = (\hat{s}_{G_{j}}^{iT} - s_{G_{j}}^{iT}) \cdot R_j^T
\end{equation}
where \(R_j\) is a rotation matrix to align a unit x vector with the jth agent’s ground truth axis at time T.
If for any prediction i, \(d^i_y\) < Thresholdlat and \(d^i_x\) < Thresholdlon the prediction is considered a correct prediction rather than a miss, otherwise a single miss is counted for prediction i. The miss rate is calculated as the total number of misses divided by the total number of objects predicted.
The thresholds change with both velocity and measurement step T as follows:
Thresholdlat | Thresholdlon | |
|---|---|---|
T = 3 seconds | 1 | 2 |
T = 5 seconds | 1.8 | 3.6 |
T = 8 seconds | 3 | 6 |
The thresholds are also scaled according to the initial speed of the agent. The scaling function is a piecewise linear function of the initial speed vi:
\begin{equation}
\mbox{Scale}(V_i) =
\begin{cases}
0.5 & \text{if $V_i <$ 1.4 m/s}\\
0.5+0.5\alpha & \text{if 1.4 m/s $< V_i <$ 11 m/s}\\
1 & \text{if $V_i >$ 11 m/s}
\end{cases}
\end{equation}
where 𝝰=(vi - 1.4) / (11 - 1.4)
The thresholds are calculated as:
Thresholdlat(vi, T) = Scale(vi) * Thresholdlat(T)
Thresholdlon(vi, T) = Scale(vi) * Thresholdlon(T)
Overlap Rate
For the purposes of this dataset challenge, the overlap rate is computed by taking the highest confidence prediction from each set of predictions for each object. If any of these predicted agent trajectories overlap at any time with any other objects that were visible at the prediction time step (compared at each time step up to T) it is considered a single overlap. The overlap rate in this challenge is computed as the total number of overlaps divided by the total number of objects predicted.
mAP
The first step to computing the mAP metric is determining a trajectory bucket for the ground truth of the objects to be predicted. The buckets include straight, straight-left, straight-right, left, right, left u-turn, right u-turn, and stationary. For each bucket, the following is computed.
Trajectory predictions are sorted by confidence value. Using the same definition of a miss as defined above, any trajectory predictions classified as a miss are assigned a false positive and any that are not considered a miss are assigned a true positive. Consistent with object detection mAP metrics, only 1 true positive is allowed for each prediction - it is assigned to the highest confidence prediction, all other predictions for the object are assigned a false positive. True positives and false positives are stored along with their confidences in a list per bucket. To compute the metric, the bucket entries are sorted and a P/R curve is computed.
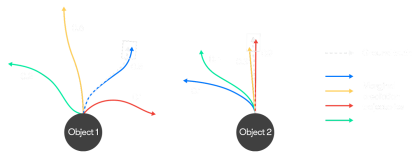
As in the above simple example for marginal prediction on two agents, the white arrows are ground truth trajectories, and the colored arrows are predicted trajectories with confidence scores. For object 1, only the blue trajectory is within the given lateral and longitudinal threshold compared to the ground truth; and for object 2, both the red trajectory and the orange trajectory are within the given lateral and longitudinal threshold. When computing the precision and recall, only the red trajectory of object 2 will be considered as true positive since the red trajectory has a higher confidence score. The precision and recall based on sorting the confidence stores can be computed as:
Rank (confidence scores) | Precision | Recall |
|---|---|---|
0.9 | 100% | 50% |
0.6 | 50% | 50% |
0.5 | 66.7% | 100% |
0.4 | 50% | 100% |
0.3 | 40% | 100% |
0.2 | 33.3% | 100% |
0.1 | 25% | 100% |
While specific models can produce probabilities over the specific trajectories, for the purpose of evaluation and in this example, we are only looking at the scores' relative ranking and do not require that they sum to 1.
The mAP metric is computed using the interpolated precision values as described in "The PASCAL Visual Object Classes (VOC) Challenge" (Everingham, 2009, p. 11) using the newer method that includes all samples in the computation consistent with the current PASCAL challenge metrics.
After an mAP metric has been computed for all trajectory shape buckets, an average across all buckets is computed as the overall mAP metric.
Soft mAP
The soft mAP metric differs from the mAP metric described above only in the way that it handles multiple matching predictions for a given trajectory. In both cases, only the highest confidence matching prediction is counted as a true positive. In the standard mAP metric, additional matching predictions count as false positives but in the soft mAP case, additional matching predictions are ignored and are not penalized as part of the metric computation. For the 2023 Motion Prediction Challenge, Soft mAP is the metric used to rank the leaderboard.
Rules Regarding Awards
Please see the Waymo Open Dataset Challenges 2023 Official Rules here.